Nội dung bài giảng
NỘI DUNG CHÍNH
| RADIAN | ĐỘ (DEGREE) | GRAD | |
| Định nghĩa | Một radian được định nghĩa là góc phụ từ tâm của đường tròn chắn một cung có độ dài bằng với bán kính của đường tròn. Cách nói khác: Độ lớn tính bằng radian của một góc phụ bằng tỷ số giữa độ dài cung và bán kính của đường tròn. | Là số đo một góc mặt phẳng. Trong đó: một vòng quay hoàn toàn là 360 độ. Cách nói khác: đó là góc ở tâm đường tròn chọn một cung tròn có chiều dài bằng 1/360 chu vi hình tròn. | Là góc ở tâm chắn một cung tròn có độ dài bằng 1/400 chu vi đường tròn. |
| Lịch sử ra đời | Radian = Radius units Thuộc hệ đơn vị SI
Roger Cotes là người đưa ra khái niệm radian vào năm 1714. Tuy nhiên, ý tưởng đo góc bằng chiều dài cung đã có từ trước đó. Ghiyath al-Kashi (khoảng 1400) dùng "phần đường kính" làm đơn vị đo góc, trong đó 1 "phần đường kính" tương đương 1/60 radian; ông cũng dùng các đơn vị nhỏ hơn bằng cách lấy các phần đường kính chia cho 60. Thuật ngữ "radian" lần đầu tiên xuất hiện trên bản in vào ngày 5 tháng 6 năm 1873 bởi James Thomson (anh của William Thomson) ở Trường Đại học Queen's, Belfast. | 1) Con số 360 có lẽ đã được chọn vì nó là số ngày trong năm của người cổ đại. Các loại lịch nguyên thủy, chẳng hạn như lịch Ba Tư sử dụng 360 ngày cho một năm.
2) Nó cũng là con số dễ dàng chia hết: nó có 22 ước số khác nhau (2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180), chia hết cho tất cả các số tự nhiên từ 2 đến 10 - ngoại trừ 7.
| Grad còn được gọi là Gon, ký hiệu là g. Vào thế kỷ 18, mét được định nghĩa là phần 10 triệu của một phần tư kinh tuyến . Do đó, một grad của chiều dài cung dọc theo bề mặt Trái đất tương ứng với 100 km (giả sử Trái đất hình cầu ); 1 centigrad của cung bằng 1 km; 0,1 cc (centi-centigrads) của cung bằng 1 mét. Đến ngày nay thì Grad ít được biết và sử dụng.
|
| Công thức | |||
| Minh họa |
| 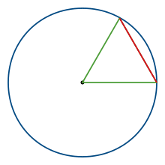 | 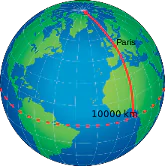 |
| Mối liên hệ | |||