Số dao động toàn phần vật thực hiện được
Vật lý 12. Dao động điều hòa. Phương trình dao động điều hòa. Chu kỳ. Tần số. Tần số góc. Tốc độ góc. Thời gian vật thực hiện được số dao động là.
Tin tức
Công thức:
Nội dung:
Khái niệm:
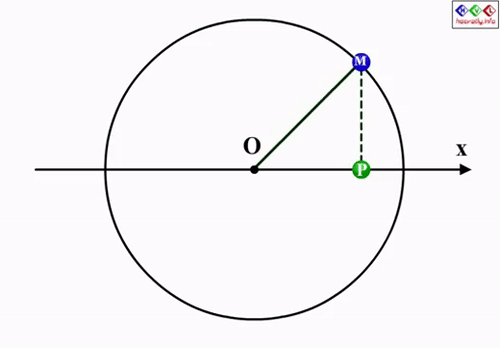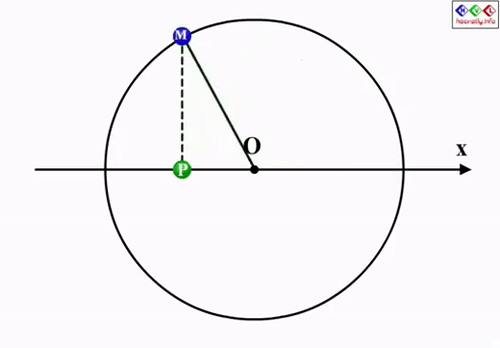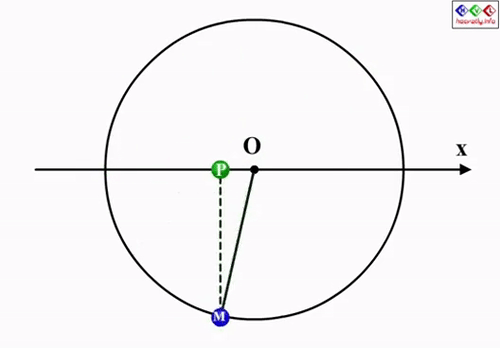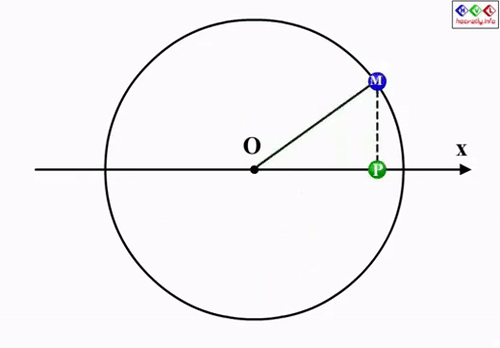
N là số dao động toàn phần vật thực hiện được. Một dao động toàn phần được tính khi vật quay về trạng thái cũ sau khi đi được trong một khoảng thời gian nào đó.
Đơn vị tính: Vòng
Tin tức
Công thức liên quan
Chu kì dao động điều hòa - vật lý 12
Vật lý 12. Dao động điều hòa. Thời gian vật thực hiện một dao động. Hướng dẫn chi tiết.
Khái niệm:
Chu kỳ của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Lưu ý:
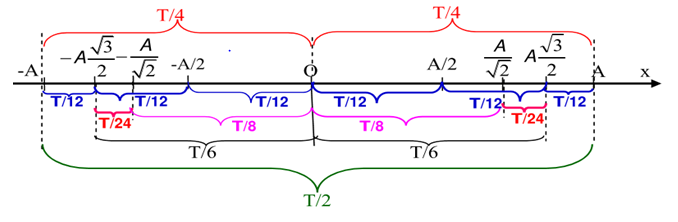
Thời gian vật đi được tại các vị trí đặc biệt:
Tần số của dao động điều hòa - vật lý 12
Vật lý 12. Dao động điều hòa. Chu kỳ. Tần số góc. Tốc độ góc. Số dao động vật thực hiện được trong một giây. Hướng dẫn chi tiết.
Khái niệm:
Tần số của dao động điều hòa là số dao động chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Biên độ dao động trong dao động điều hòa - vật lý 12
Vật lý 12. Biên độ dao động. Dao động điều hòa. Quỹ đạo. Quãng đường vật đi được. Công thức liên hệ giữa các đại lượng. Hướng dẫn chi tiết.
Chú thích:
: Li độ của chất điểm
: Độ dài quỹ đạo
: Quãng đường vật đi được trong vòng
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: số dao động toàn phần mà chất điểm thực hiện được
: Vận tốc của chất điểm tại vị trí có li độ
: Gia tốc của chất điểm tại vị trí có li độ x
: Vận tốc cực đại của chất điểm
: Gia tốc cực đại của chất điểm
Chứng minh các công thức:
+ Vật chuyển động trên quỹ đạo dài .
+ Vật chuyển động cứ một vòng sẽ đi được quãng đường là , vật vật đi vòng thì quãng đường sẽ là .
+ Từ công thức tốc độ cực đại của vật: .
+ Từ công thức gia tốc cực đại của vật: .
+ Ta có: và .
+ Từ hệ thức độc lập thời gian :.
+ Từ hệ thức độc lập thời gian :.
Chu kỳ của con lắc lò xo - vật lý 12
Vật lý 12. Dao động điều hòa. Chu kỳ của con lắc lò xo. Hướng dẫn chi tiết.
Khái niệm:
Chu kỳ của lắc lò xo dao động điều hòa là khoảng thời gian vật thực hiện được một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
: Khối lượng vật treo trên lò xo .
: Độ cứng của lò xo .
: Gia tốc trọng trường .
: Độ biến dạng của lò xo tại vị trí cân bằng .
Lưu ý:
Ta có :
Tần số dao động của con lắc lò xo - vật lý 12
Vật lý 12. Dao động điều hòa. Tần số dao động. Con lắc lò xo. Chu kỳ dao động. Tần số góc Hướng dẫn chi tiết.
Khái niệm:
Tần số dao động là số dao động và chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Tần số quay đều của thanh - vật lý 12
Vật lý 12.Công thức tính tần số quay đều của thanh. Hướng dẫn chi tiết.
Công thức :
Với : tần số quay của thanh .
: tốc độ góc .
N: số vòng
t : thời gian
Công thức tính năng lượng cần cung cấp cho mỗi chu kì của dao động duy trì - vật lý 12
Vật lý 12.Công thức tính năng lượng cần cung cấp cho mỗi chu kì của dao động duy trì. Hướng dẫn chi tiết.
Công thức :
Độ giảm năng lượng của dao động sau 1 chu kì :
Sau N chu kì
Năng lượng cần cung cấp sau N chu kì :
Công suất cung cấp năng lượng:
Công thức tính thời gian giữa hai lần trùng phùng - vật lý 12
Khoảng cách hai lần trùng phùng
Vật lý 12,Công thức tính thời gian giữa hai lần trùng phùng, Hướng dẫn chi tiết.
Để xác định chu kỳ của một con lắc lò xo (con lắc đơn) người ta so sánh với chu kỳ (đã biết) của một con lắc khác .
Hai con lắc gọi là trùng phùng khi chúng đồng thời đi qua một vị trí xác định theo cùng một chiều.
Gọi thời gian giữa hai lần trùng phùng liên tiếp là . Ta có:
(với và là số dao động con lắc 1 và 2 thực hiện trong thời gian )
Ta chứng minh được thời gian giữa hai lần trùng phùng là:
* Lưu ý: Công thức trên chỉ đúng cho con lắc trùng phùng; còn nếu đề bài cho không thỏa mãn điều kiện trên thì ta dùng công thức: 2 con lắc gặp nhau khi ở cùng vị trí: x1 = x2 từ đó giải ra thời gian .