Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng
Dạng bài: Khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng. Hướng dẫn chi tiết.
Tin tức
Tại nơi có gia tốc trọng trường g, con lắc đơn dao động điều hòa với biên độ góc nhỏ. Lấy mốc thế năng ở vị trí cân bằng, khi con lắc chuyển động nhanh dần theo chiều dương đến vị trí có động năng bằng thế năng thì li độ góc của con lắc bằng
Công thức liên quan
Tỉ số động năng và thế năng trong dao động điều hòa - vật lý 12
Vật lý 12.Tỉ số động năng và thế năng trong dao động điều hòa. Hướng dẫn chi tiết.
Công thức:
Tỉ số động năng và thế năng con lắc đơn - vật lý 12
Vật lý 12.Tỉ số động năng và thế năng con lắc đơn. Hướng dẫn chi tiết.
Công thức :
Biến số liên quan
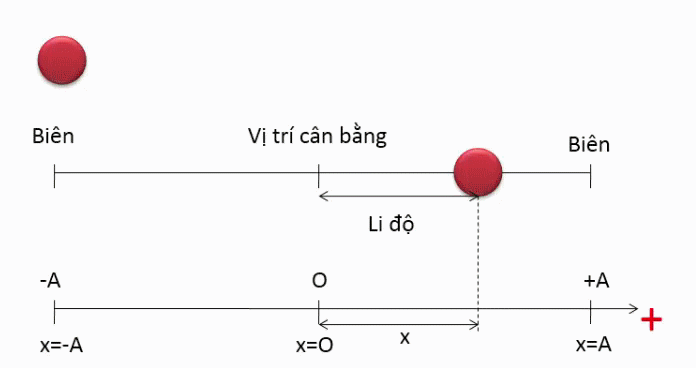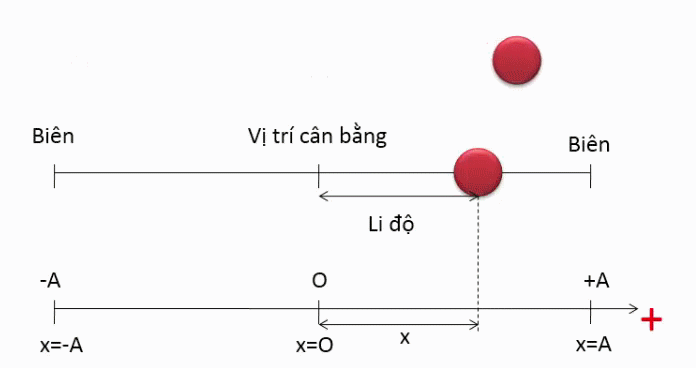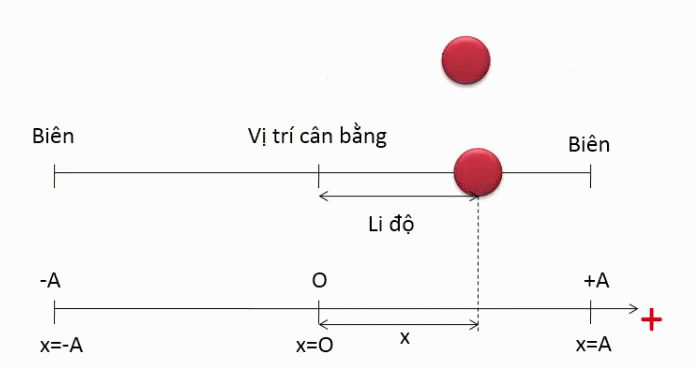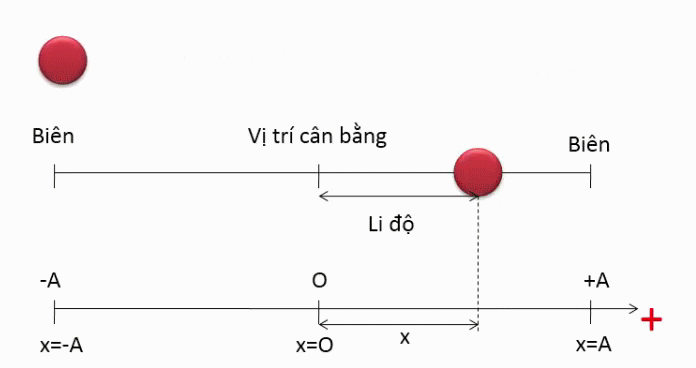
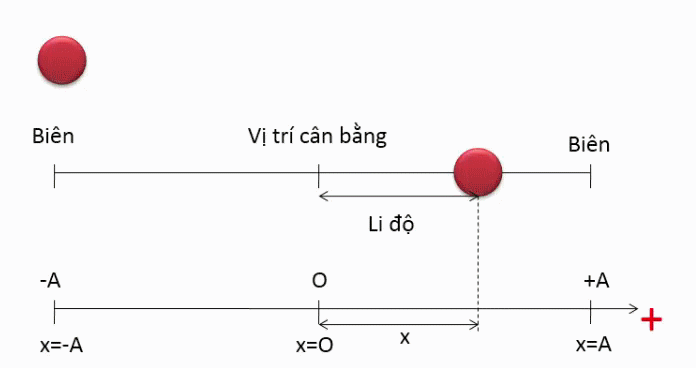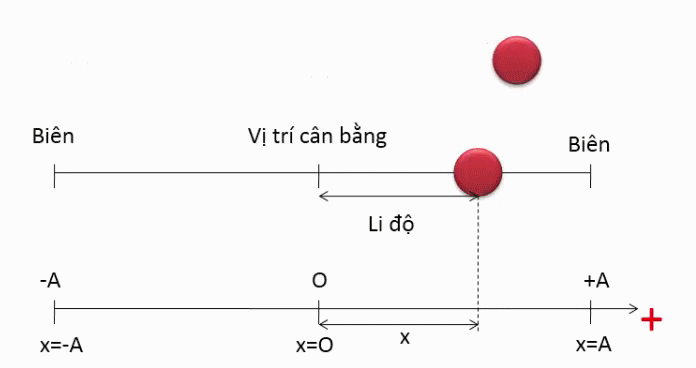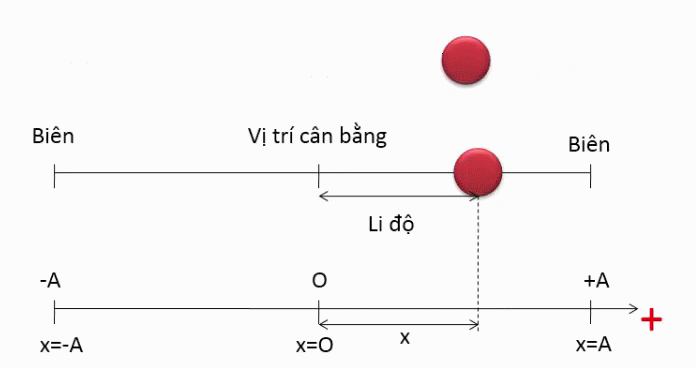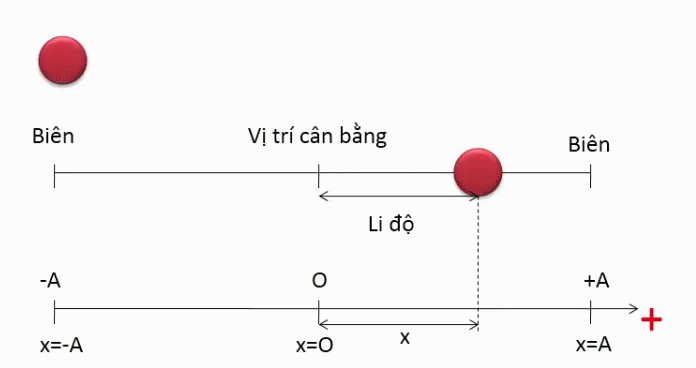
Li độ của chất điểm trong dao động điều hòa
Li độ của chất điểm trong dao động điều hòa. Phương trình li độ. Dao động điều hòa
Khái niệm:
- Li độ hay độ dời là khoảng cách ngắn nhất từ vị trí ban đầu đến vị trị hiện tại của vật chuyển động, thường được biểu diễn tọa độ của vật trong hệ quy chiếu khảo sát chuyển động.
- Li độ trong dao động điều hòa là hàm và đồ thị là hình . Li độ có thể âm hoặc dương tùy thuộc vào pha dao động của vật.
Đơn vị tính: hoặc
Biên độ của dao động điều hòa
Phương trình dao động điều hòa. Biên độ của dao động điều hòa.
Khái niệm:
- Biên độ là li độ cực đại của vật đạt được.
- Biên độ là khoảng cách xa nhất mà vật có thể đạt được, với gốc tọa độ thường được chọn tại vị trí cân bằng.
- Biên độ là một đại lượng vô hướng, không âm đặc trưng cho độ lớn của dao động.
Đơn vị tính: hoặc
Vận tốc của chất điểm trong dao động điều hòa
Vận tốc vật. Vận tốc chất điểm trong dao động điều hòa. Dao động điều hòa. Phương trình vận tốc trong dao động điều hòa
Khái niệm:
là vận tốc của chất điểm trong dao động điều hòa, là đạo hàm của li độ theo thời gian.
Đơn vị tính:
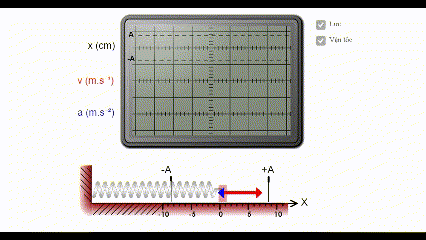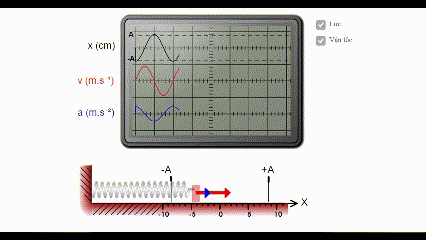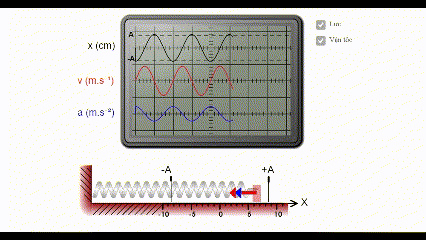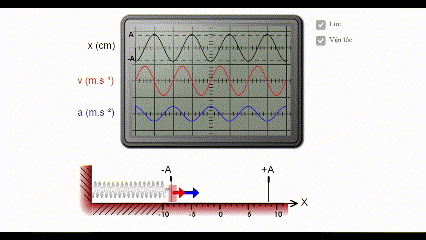
Vận tốc cực đại của chất điểm trong dao động điều hòa
Vật lý 12. Dao động điều hòa. Phương trình dao động điều hòa. Chu kỳ. Tần số. Tần số góc. Tốc độ góc. Biên độ dao động
Khái niệm:
Vận tốc của vật dao động điều hòa có độ lớn cực đại khi vật đi qua vị trí cân bằng, tức là li độ của vật lúc này bằng 0.
Đơn vị tính:
Thế năng của con lắc đơn trong dao động điều hòa - Vật lý 12
Vật lý 12.Thế năng của con lắc đơn trong dao động điều hòa. Hướng dẫn chi tiết.
Khái niệm:
Thế năng của con lắc đơn là dạng năng lượng của con lắc có được khi vật được đặt trong trọng trường và phụ thuộc vào vị trí so với gốc thế năng. Người ta thường chọn gốc thế năng ở vị trí con lắc cân bằng.
Đơn vị tính: Joule
Động năng của dao động điều hòa - Vật lý 12
Vật lý 12.Động năng của dao động diều hòa. Hướng dẫn chi tiết.
Khái niệm:
Động năng của dao động điều hòa là năng lượng của vật dao động điều hòa có được khi chuyển động
Đơn vị tính: Joule
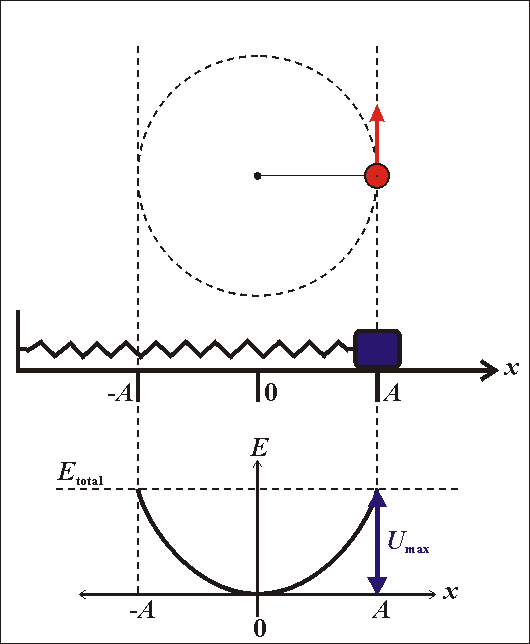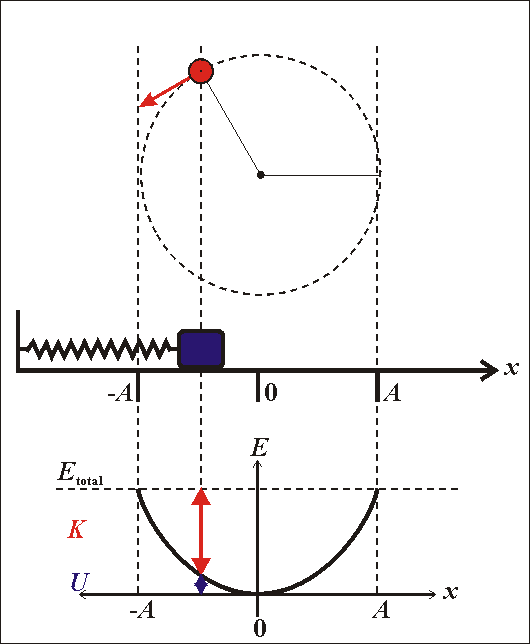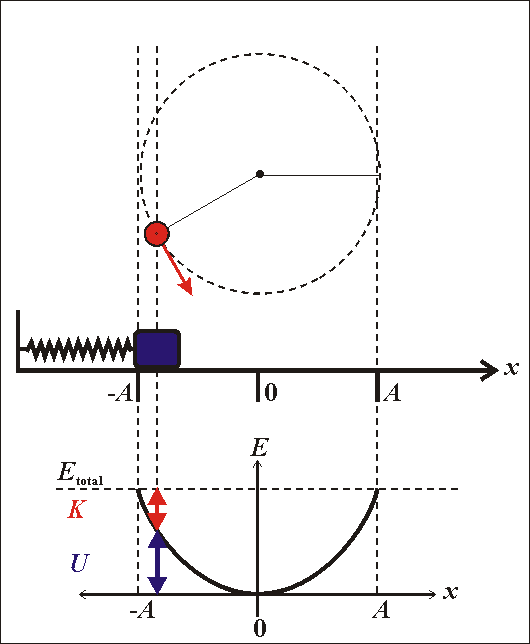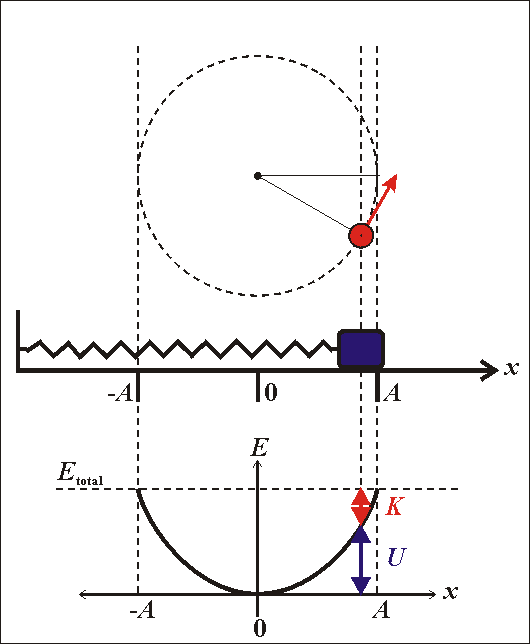
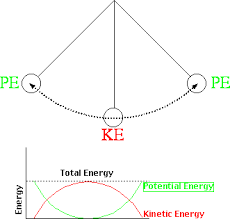
Cơ năng của dao động điều hòa - Vật lý 12
Vật lý 12.Cơ năng của dao động điều hòa.Hướng dẫn chi tiết
Khái niệm:
Cơ năng của dao động điều hòa là tổng các dạng năng lượng động năng và thế năng của vật khi đang dao động điều hòa. Cơ năng được bảo toàn khi bỏ qua ma sát.
Đơn vị tính: Joule (J)
Các câu hỏi liên quan
Hình 1.3 là đồ thị độ dịch chuyển - thời gian của ô tô chuyển động thẳng theo một hướng xác định. Ô tô đi với tốc độ lớn nhất trong đoạn đường nào?
- Tự luận
- Độ khó: 0
Hình 1.3 là đồ thị độ dịch chuyển - thời gian của ô tô chuyển động thẳng theo một hướng xác định. Ô tô đi với tốc độ lớn nhất trong đoạn đường nào?
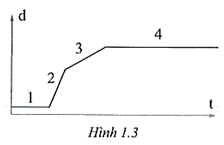
A. 1.
B. 2.
C. 3.
D. 4.
Một con nhện bò dọc theo hai cạnh của một chiếc bàn hình chữ nhật. Biết hai cạnh bàn dài 0,8 m và 1,2 m. Độ dịch chuyển của con nhện khi đi được 2,0 m là bao nhiêu?
- Tự luận
- Độ khó: 0
Một con nhện bò dọc theo hai cạnh của một chiếc bàn hình chữ nhật. Biết hai cạnh bàn có chiều dài lần lượt là 0,8 m và 1,2 m. Độ dịch chuyển của con nhện khi nó đi được quãng đường 2,0 m là
A.1,4 m. B. 1,5 m. C. 1,6 m. D. 1,7 m.
Bảng 2 mô tả các đoạn đường khác nhau trong một cuộc đi bộ. Trong mỗi giai đoạn, người đi bộ đi trên đường thẳng với tốc độ ổn định và một hướng xác định.
- Tự luận
- Độ khó: 0
Bảng 2 mô tả các đoạn đường khác nhau trong một cuộc đi bộ. Trong mỗi đoạn, người đi bộ đi trên đường thẳng với tốc độ ổn định và một hướng xác định.
Bảng 2
|
Đoạn đường |
Độ dài đoạn đường (m) |
Thời gian đi (s) |
Hướng đi |
|
1 |
25 |
8 |
B |
|
2 |
21 |
8 |
T |
|
3 |
28 |
6 |
N |
|
4 |
12 |
5 |
Đ |
a) Trong đoạn đường nào, người đi bộ chuyển động nhanh nhất? Giải thích.
b) Dùng giấy kẻ ô vuông, vẽ biểu đồ thể hiện đường đi bộ theo hướng và tỉ lệ như bảng 2. Dùng biểu đồ để tìm độ dịch chuyển giữa điểm bắt đầu và điểm kết thúc hành trình.
c) Dùng kết quả ở b) và số liệu ở bảng 2 để tìm vận tốc trung bình trong cả quãng đường đi bộ.
d) Giải thích tại sao người đi bộ không có vận tốc tính ở c) tại bất kì điểm nào của chuyến đi.
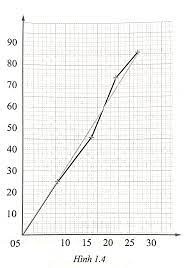
e) Một học sinh đã tính vận tốc trung bình bằng cách vẽ đồ thị quãng đường đi được theo thời gian như thể hiện ở hình 1.4. Dựa vào đồ thị này, học sinh ấy tính vận tốc trung bình như sau:
vận tốc trung bình = = 3,2 m/s
Học sinh đã làm đúng hay sai? Vì sao?
Một người đi bộ 3,0 km theo hướng nam rồi 2,0 km theo hướng tây. Vẽ giản đồ vectơ để minh hoạ các độ dịch chuyển. Tính độ dịch chuyển tổng hợp.
- Tự luận
- Độ khó: 0
Một người đi bộ 3,0 km theo hướng nam rồi 2,0 km theo hướng tây.
a) Vẽ giản đồ vectơ để minh hoạ các độ dịch chuyển.
b) Tìm độ dịch chuyển tổng hợp.
Một người điều khiển thuyền đi được 5,6 km theo hướng bắc trên mặt hồ phẳng lặng trong thời gian 1,0 h. Tìm độ dịch chuyển tổng hợp của thuyền. Xác định vận tốc trung bình của chuyến đi.
- Tự luận
- Độ khó: 0
Một người điều khiển thuyền đi được 5,6 km theo hướng bắc trên mặt hồ phẳng lặng trong thời gian 1,0 h. Sau đó, anh ta quay thuyền đi về phía tây 3,4 km trong 30,0 phút.
a) Tìm độ dịch chuyển tổng hợp của thuyền.
b) Xác định vận tốc trung bình của chuyến đi.